Vật lý lý thú: lời giải sai ở đâu?

Dưới đây là lời giải sai của một bài toán mà mình luôn canh cánh trong lòng từ 14 năm trước. Lý do là: bài toán này được in trong hai cuốn sách: "Cơ học 1" của thầy Tô Giang và " Bồi dưỡng học sinh giỏi vật lý trung học phổ thông - Bài tập Cơ học - Nhiệt học" của nhóm tác giả thầy Vũ Thanh Khiết, tuy nhiên hai cuốn sách lại đưa ra hai đáp số khác nhau, và dưới đây là các lời giải chưa chính xác mà mình tổng hợp được. Cho tới gần đây, khi lật xem lại thì cuối cùng mình đã giải quyết được hoàn toàn vấn đề này.

Trước khi đi vào tìm hiểu, cần làm rõ là: việc ai đúng ai sai không quan trọng, thậm chí các lời giải sai còn mang lại cho chúng ta nhiều hiểu biết hơn cả các lời giải đúng, mục đích cuối cùng của tìm tòi là sự hiểu biết, không phải trở thành người luôn đúng. Dưới đây là đề bài và cách giải sai:

Đề bài

Một dây xích AB, dài $l$ có một phần nằm trên mặt bàn nằm ngang, nhẵn và một phần dài $h$ lơ lửng ở ngoài. Đầu B của dây chạm nhẹ vào mặt bàn (hình vẽ). Người ta thả đầu A của xích. Tìm tốc độ của đầu A khi nó vừa rời khỏi mặt bàn.

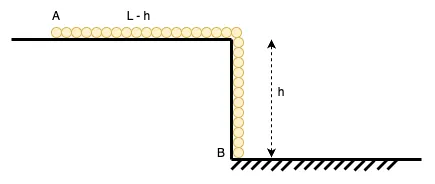Hình 1

Lời giải SAI

Gọi $M$ là khối lượng của sợi dây xích. Giả sử ở thời điểm $t$, đầu trên $A$ của xích dịch chuyển tới 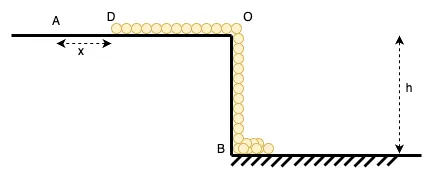$D$, với $AD = x$. Hình 2

Theo định lí biến thiên động lượng:

$$dp = d(mv) = mdv + vdm = Fdt \tag{1}$$

trong đó $m$ là khối lượng phần xích BOD:

$$m = \frac{M}{l}(l-x) \implies dm = -\frac{M}{l}dx$$

còn $F$ là trọng lượng của phần xích OB: $F = \frac{M}{l}hg$

Thay $m, dm, F$ vào (1), ta có:

$$\begin{align*} \frac{M}{l}(l-x)dv - \frac{Mv}{l}dx &= \frac{M}{l}hgdt \\[0.2in] (l-x)dv - vdx &= hgdt \tag{2} \end{align*}$$

từ:

$$v = \frac{dx}{dt} \implies dt = \frac{dx}{v} \tag{3}$$

Thay (3) vào (2) ta được:

$$\begin{align*} (l-x)dv - vdx &= \frac{gh}{v}dx \\[0.2in] (l-x)dv &= \bigg(v + \frac{gh}{v} \bigg) dx \\[0.2in] \frac{dv}{v + \frac{gh}{v}} &= \frac{dx}{l-x} \\[0.2in] \frac{vdv}{v^2 + gh} &= \frac{dx}{l-x} \end{align*}$$

Lấy tích phân hai vế:

$$\begin{align*} \int_0^v\frac{vdv}{v^2 + gh} &= \int_0^{l-h}\frac{dx}{l-x} \\[0.2in] \int_0^v\frac{d(v^2)}{v^2 + gh} &= \int_0^{l-h}\frac{2dx}{l-x} \\[0.2in] ln(gh+v^2)\Big|_0^v &= -2ln(l-x)\Big|_0^{l-h} \\[0.2in] ln\frac{gh+v^2}{gh} &= -2 ln\frac{h}{l} \\[0.2in] 1+\frac{v^2}{gh} &= \frac{l^2}{h^2} \\[0.2in] v^2 &= gh \bigg(\frac{l^2}{h^2} -1\bigg) \end{align*}$$

Cuối cùng ta được:

$$v = \sqrt{gh \bigg(\frac{l^2}{h^2} -1\bigg)}$$

Kết quả này là sai, nhưng sai ở chỗ nào?

Lời giải SAI thứ 2

Trước hết, đặt $\lambda = \frac{M}{l}$

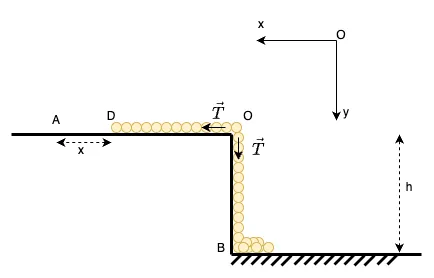Hình 3

Gọi $\vec{T}$ là lực căng của sợi xích tại giao điểm như hình. Áp dụng định lý biến thiên động lượng lần lượt đối với hệ xích OB và OD, chiếu lên hệ toạ độ Oxy ta được:

$$\begin{align*} m_{OD}dv + v(dm_{OD}) &= Tdt \\[0.2in] m_{OB}dv + vd(m_{OB}) &= ( m_{OB} g - T) dt \end{align*}$$

Lưu ý: lực $\vec{T}$ hướng xuống dưới góp phần kéo phần xích OD, lực $\vec{T}$ hướng sang trái góp phần kéo phần xích OB "lên", đại diện cho quán tính của phần xích OD, dấu của $\vec{v}$ và $\vec{T}$ ở hai phương trình trên được thay đổi cho dễ nhìn, không làm thay đổi tính chính xác của vật lý và toán. Thay $\lambda$ ở trên ta được:

$$\begin{align} \lambda (l - x - h)dv + v(-\lambda dx) &= Tdt \tag{4} \\[0.2in] \lambda hdv &= ( \lambda gh - T) dt \tag{5} \end{align}$$

Cộng từng vế của (4) và (5), ta được:

$$\begin{align*} \lambda (l - x)dv - \lambda vdx &= \lambda ghdt \\[0.2in] (l - x)dv - vdx &= ghdt \tag{6} \end{align*}$$

Ta thấy rằng (6) chính là (2), vì vậy, tiếp tục giải như trên, ta nhận được kết quả sai tương tự, kết quả này là sai, nhưng sai ở chỗ nào?

Lời giải trông có vẻ đúng thứ 3

Áp dụng định luật II Newton lần lượt đối với hệ xích OB và OD, chiếu lên hệ toạ độ Oxy ta được:

$$\begin{align*} m_{OB} \frac{dv}{dt} &= T \\[0.2in] m_{OD} \frac{dv}{dt} &= m_{OD}g - T \end{align*}$$

Thay khối lượng của từng phần OB và OD:

$$\begin{align*} \lambda (l - x - h) \frac{dv}{dt} &= T \tag{7} \\[0.2in] \lambda h \frac{dv}{dt} &= \lambda gh - T \tag{8} \end{align*}$$

Cộng từng vế của (7) và (8), ta được:

$$\begin{align*} \lambda (l - x) \frac{dv}{dt} &= \lambda gh \\[0.2in] \lambda (l - x) dv &= \lambda gh dt \\[0.2in] \lambda (l - x) dv &= \lambda gh \frac{dx}{v} \\[0.2in] vdv &= \frac{ghdx}{l-x} \\[0.2in] \end{align*}$$

Lấy tích phân hai vế:

$$\begin{align*} \int_0^vvdv &= gh \int_0^{l-h}\frac{dx}{l-x} \\[0.2in] \int_0^vd(v^2) &= 2gh \int_0^{l-h}\frac{dx}{l-x} \\[0.2in] v^2\Big|_0^v &= -2ghln(l-x)\Big|_0^{l-h} \\[0.2in] v^2 &= -2gh ln\frac{h}{l} \\[0.2in] v^2 &= 2gh ln\frac{l}{h} \\[0.2in] v &= \sqrt{2gh ln \frac{l}{h}} \end{align*}$$

Theo bạn, kết quả này có đúng không?

Lời giải trông có vẻ đúng thứ 4

Đây là lời giải trong sách Cơ học 1, lưu ý đoạn ống được bọc phía trên, tại sao thêm phần ống này vào lại không thay đổi kết quả? Điều này gợi ý điều gì?

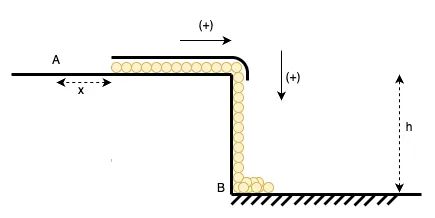Hình 4

Xét đoạn xích đang chuyển động. Đây là một hệ có khối lượng giảm dần, vì cứ sau khoảng thời gian $dt$ lại có một mắt xích dài $dx$ rời khỏi hệ và nằm yên trên bàn. Do cấu tạo của xích mà mắt xích này không tác dụng trở lại hệ một lực nào. Vì thế ta xét hệ là đoạn xích đang chuyển động trừ mắt xích này. Việc tách một mắt xích chuyển động khỏi hệ không ảnh hưởng gì đến kết quả cần tìm. Áp dụng định luật II Newton:

$$m_t \frac{dv}{dt} = \sum F_{ext} + \frac{dm}{dt} u \tag{9}$$

trong đó:

$$\begin{cases} \begin{align*} m_t &= \frac{m}{l}(l - x) \\[0.2in] u &= 0 \\[0.2in] \sum F_{ext} &= \frac{m}{l} gh \end{align*} \end{cases}$$

Thay vào (9):

$$\begin{align*} \frac{m}{l} (l-x) \frac{dv}{dt} &= \frac{m}{l} gh + 0 \\[0.2in] (l-x) \frac{dv}{dt} &= gh \\[0.2in] (l-x)dv &= gh dt \\[0.2in] (l-x)dv &= gh \frac{dx}{v} \\[0.2in] vdv &= gh \frac{dx}{l-x} \\[0.2in] \frac{1}{2} d(v^2) &= -gh \frac{dx}{l-x} \\[0.2in] \end{align*}$$

Tich phân 2 vế:

$$\begin{align*} \frac{1}{2} \int_0^v d(v^2) &= -gh \int_0^{l-h} \frac{d(l-x)}{l-x} \\[0.2in] \frac{1}{2} v^2 &= gh ln\frac{l}{h} \\[0.2in] v &= \sqrt{2gh ln\frac{l}{h} } \\[0.2in] \end{align*}$$

Kết quả này giống với kết quả ở cách giải thứ 3, theo bạn, kết quả này có đúng không?

Lời giải trông có vẻ đúng thứ 5

Trường hợp 1: không có phần bọc phía trên

Hình 5

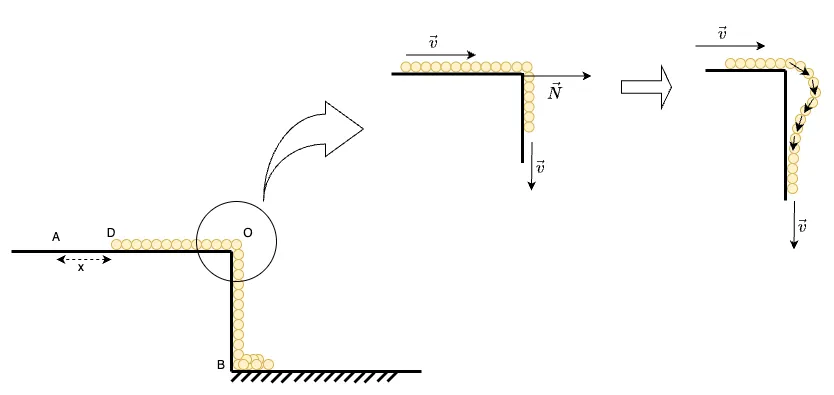
Trước tiên, xem xét khu vực mép của bàn. Áp dụng định lý biến thiên động lượng cho hệ cả dây xích $l$ với phương ngang ta có:

$$d\vec{P_x} = \vec{F_?} dt$$

Từ trạng thái đầu (tĩnh) cho đến có vận tốc, động lượng phương ngang cả hệ tăng dần, suy ra bắt buộc phải có một ngoại lực có thành phần theo phương ngang tác động lên hệ. Trực giác giúp ta thấy rằng phản lực từ mép bàn là tác nhân khả dĩ nhất gây ra động lượng này. Và chính nhờ động lượng này mà các mắt xích có xu hướng văng ra khỏi mép bàn (hình 5).

Hình 6

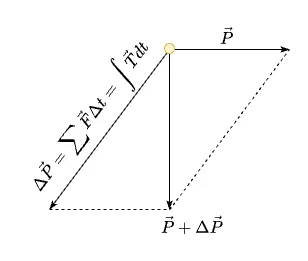
Hình 6 cho một cái nhìn trực quan về sự thay đổi động lượng của mỗi mắt xích từ khi hoàn toàn trên mặt bàn đến khi hoàn toàn chuyển động hướng xuống dưới. Ở đây lực căng $\vec{T}$ biến đổi hướng liên tục theo một quỹ đạo không rõ ràng (Hình 5) khiến việc tính tích phân là rất khó khăn. Việc tính toán này cũng không cần thiết khi ta chỉ tìm vận tốc cuối cùng dọc theo chiều thẳng đứng của sợi xích

Vì sự liên kết giữa các mắt xích với lực căng $\vec{T}$, động lượng này sẽ bị triệt tiêu dần theo hướng ngược lại và thay đổi hướng, từ phương ngang thành phương thẳng đứng. Việc tính toán các thành phần này là không khả thi trong bài toán này vì ta không có thông tin vật lý về kết cấu của sợi xích.

Hình 7

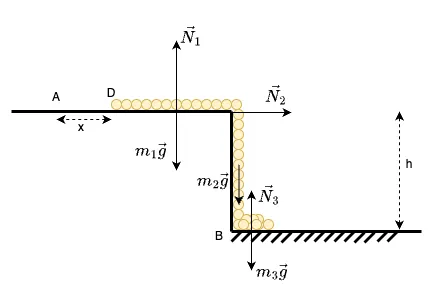
Như vậy, tóm lại ta có toàn bộ các lực tác động lên hệ như hình 7. Phản lực $\vec{N_1}$ cân bằng với khối lượng của phần xích OD, không có tác động vật lý gây ra chuyển động của xích nên có thể bỏ qua. Phản lực $\vec{N_3}$ cân bằng với phần xích OD và triệt tiêu động lượng của các phần tử xích rời xuống sàn. Như vậy ta có:

$$\vec{N_3} = m_3\vec{g} + \Delta \vec{N_3}$$

Trong đó phần $\Delta\vec{N_3}$ được tách riêng ra đại diện cho sự "hấp thụ" động lượng của mặt đất đối với sợi xích.

Xét hệ là toàn bộ sợi xích $l$, áp dụng định lý biến thiên động lượng theo phương thẳng đứng, theo hình 7, ta có:

$$\begin{align*} ( m_2 \vec{g} - \Delta \vec{N_3}) dt &= d\vec{P} \\[0.2in] \lambda h g dt - \Delta N_3 dt &= m_2 dv \tag{10} \end{align*}$$

Ta thấy phần xích $m_3$ có độ dài bằng phần dịch chuyển $x$ ở đoạn A, vì vậy:

$$dP_{m3} = \Delta N_3 dt = v dm = \lambda v dx$$

Phần động lượng của $m_3$ bị mất cân bằng với phản lực $\vec{N}_3$ của mặt đất và trọng lực $m_3\vec{g}$, không có tác động vật lý tới hệ xích đang chuyển động. Thay vào (10) ta được:

$$\begin{align*} \lambda h g dt - \lambda v dx &= \lambda h dv \\[0.2in] g dt - \frac{v}{h} dx &= dv \\[0.2in] g \frac{dx}{v} - \frac{v}{h} dx &= dv \\[0.2in] dv &= dx \bigg( \frac{g}{v} - \frac{v}{h} \bigg) \\[0.2in] \frac{hv dv}{gh - v^2} &= dx \\[0.2in] \frac{h}{2} \int_0^v \frac{d(v^2)}{gh-v^2} &= \int_0^{l-h} dx \\[0.2in] -ln(gh - v^2)\bigg|_0^v &= \frac{2}{h} x \bigg|_0^{l-h} \\[0.2in] ln \bigg(\frac{gh}{gh-v^2} \bigg) &= 2\bigg(\frac{l}{h} - 1 \bigg) \\[0.2in] \frac{gh}{gh-v^2} &= e^ {\displaystyle {2 \bigg(\frac{l}{h} - 1 \bigg) }} \\[0.2in] 1 - \frac{v^2}{gh} &= e^ {\displaystyle {2 \bigg( 1 - \frac{l}{h} \bigg) }} \\[0.2in] v &= \sqrt { gh \Bigg[ 1 - e^{ \displaystyle{2 \Big( 1 - \frac{l}{h} \Big) }} \Bigg] } \\[0.2in] \end{align*}$$

Có thể thấy điểm khác biệt lớn nhất của kết quả này so với các kết quả trên là $v$ không tiến đến vô cực khi $l/h$ tiến đến vô cực nữa mà bị giới hạn bởi $\sqrt{gh}$, điều này gợi ý điều gì? Liệu kết quả này có đúng về mặt vật lý không?

$$\lim_{ \frac{l}{h} \rightarrow \infin} \sqrt { gh \Bigg[ 1 - e^{ \displaystyle{2 \Big( 1 - \frac{l}{h} \Big) }} \Bigg] } = \sqrt{gh} \tag{11}$$

Trường hợp 2: có phần bọc phía trên

Hình 8

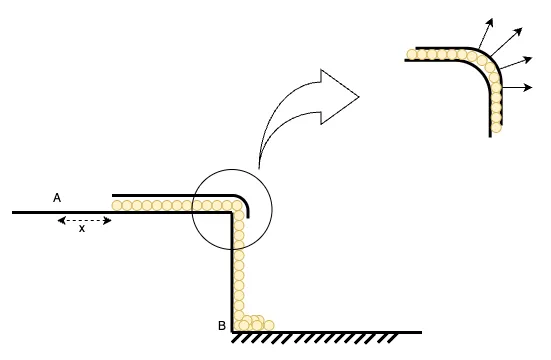
Tiếp tục xét trường hợp có đoạn ống bọc phía trên (hình 8). Nhờ đoạn ống này, các mắt xích không còn văng ra khỏi mép bàn nữa, động lượng theo phương ngang của chúng không tự biến mất mà chúng bị triệt tiêu bởi phản lực của thành ống. Với giả thiết các thành phần xích và thành ống có độ cứng vô hạn, như vậy toàn bộ động lượng theo phương ngang sẽ được điều hướng thành phương thẳng đứng (?). Nhờ lực này mà phương trình (10) trở thành:

$$\lambda h g dt - \Delta N_3 dt + F_{\text{ống}} dt = m_2 dv \tag{12}$$

Lực trên thành ống có thể không đồng đều về cả độ lớn và hướng, tuy nhiên có thể sử dụng giả thiết bảo toàn tất cả động lượng ở trên để có $F_{\text{ống}} dt = v dm$, thay vào (12):

$$\begin{align*} \lambda h g dt - \Delta N_3 dt + vdm &= m_2 dv \\[0.2in] \lambda h g dt - vdm + vdm &= m_2 dv \\[0.2in] \lambda h g \frac{dx}{v} &= \lambda h dv \\[0.2in] v dv &= gdx \\[0.2in] \int_0^v d(v^2) &= 2g \int_0^{l-h} dx \\[0.2in] v^2 &= 2 g (l-h) \\[0.2in] v &= \sqrt{2gh \bigg( \frac{l}{h} - 1 \bigg) } \tag{13} \end{align*}$$

Kết quả này có đặc điểm tương tự bốn kết quả đầu tiên là $v$ tiến đến vô cực khi $l/h$ tiến đến vô cực. Điều này là phù hợp với giả thiết vì lúc này sợi xích tương tự một vật được gia tốc liên tục bằng lực $\lambda h\vec{g}$ mà năng lượng không bị hao tổn trong toàn bộ quá trình.

Các lời giải sai ở đâu?

Từ các phân tích trên, có thể thấy các lỗi sai của từng lời giải như sau:

Lời giải thứ 1:

• Coi động lượng là một đại lượng vô hướng thay vì có hướng.
• Áp dụng định lý biến thiên động lượng với một hệ "không gian" thay vì hệ vật chất.
• Bỏ qua lực từ thành bàn tác động lên hệ.

Lời giải thứ 2:

• Áp dụng định lý biến thiên động lượng với một hệ "không gian" thay vì hệ vật chất.

Lời giải thứ 3:

• Bỏ qua lực từ thành bàn tác động lên hệ.
• Áp dụng định luật II Newton với một hệ có khối lượng biến đổi.

Lời giải thứ 4:

• Bỏ qua các thành phần lực từ thành ống tác động lên hệ.

Lời giải thứ 5:

• ???

Lời giải thứ 5 sẽ được coi là đúng cho đến khi có lỗi sai được tìm ra!

Nhưng...

Nhìn vào phương trình (10), giả sử ta thêm lực ma sát vào mặt sàn bên trên, (10) không hề thay đổi, vì lực ma sát chỉ có tác động theo phương ngang! Điều này dẫn đến vấn đề, dù lực ma sát có lớn bao nhiêu thì kết quả của chúng ta vẫn không thay đổi. Thật phi lý!

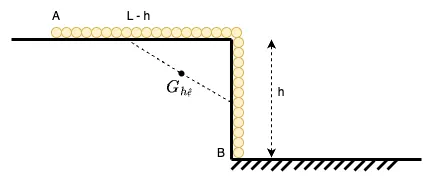Hình 9

Nếu nhìn hệ dưới góc nhìn một vật có khối tâm $G$, rõ ràng trọng lực $m_2\vec{g}$ là một lực có tác động gây ra mô men xoắn xung quanh $G$, tức là phần xích trên bàn phía trên sẽ luôn có xu hướng văng ra ngoài (tất nhiên điều này là không hoàn toàn chính xác vì dây xích không phải là vật rắn). Điều này dẫn đến các phân tích phía dưới đây.

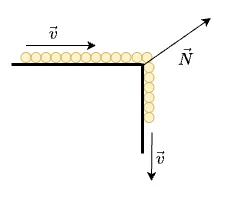Hình 10

Nếu mặt bàn phía trên không có lực ma sát, sự phi lý này chưa thể hiện rõ ràng, vì lúc đó xích sẽ văng ra khỏi mép ngay khi bắt đầu chuyển động. Nhưng khi có lực ma sát thì ngược lại, theo trực giác, ma sát sẽ cùng với trọng lực $m_2\vec{g}$ kéo xích ép vào mép bàn, điều này vô hình chung kéo cả hệ chạy chậm lại, kết quả không thể không thay đổi được!

Để giải quyết sự phi lý này, phản lực $\vec{N}$ phải có xu hướng hướng lên như trong hình 10, chứ không thể chỉ có thành phần theo phương ngang được, và do đó dây xích có xu hướng siết chặt và bào mòn mép bàn, khiến mép bàn không thể vuông như đề bài, mép bàn phải cong thì mới hợp lý!

Ngay cả khi chấp nhận tất cả sự phi lý của mép bàn, thì (10) vẫn không chính xác, vì khi xích văng khỏi bàn, nó không còn căng nữa, khi đó, các thành phần vận tốc của từng phần tử trên xích không phải $v$ thuần túy, mà thay đổi theo vị trí, lúc đó bài toán rơi vào trạng thái không thể giải được bằng các công cụ toán học đơn giản của chúng ta. Để giải được, ta buộc phải đưa ra các giải thuyết phi lý, và sự phi lý này sẽ chỉ đưa đến các kết quả tính toán phi lý. Từ nhận định này, bài toán như hình (11) được đề xuất thay thế. Việc thay thế đề bài là cần thiết vì:

Trong tay chúng ta chỉ có các phương trình vật lý chứ không có các phương trình phi vật lý, do vậy, một đề bài phi lý là không thể giải được.

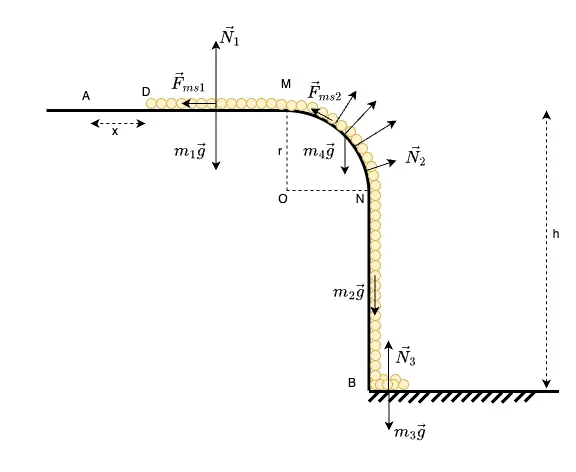Hình 11

Trong hình 11, giả sử hệ số ma sát là $\mu$ và bán kính mép bàn phần cong là $r$. Và với giả thiết là lực ma sát đủ lớn để khiến xích không bị văng ra ngoài theo phương ngang. Lời giải của bài toán này như sau: ....