Tạo mô hình 3D cơ thể người bằng AI với Flow Matching

Gần đây mình có tìm hiểu về Flow Matching - một mô hình xác suất để xây dựng giải pháp generative AI. Mỗi một mô hình giải pháp là một tư duy triết học về cách phân tích và giải quyết vấn đề. Để hiểu bản chất của chúng, cách duy nhất là tìm cách vận dụng chúng vào một bài toán cụ thể. Ok, cùng chọn một bài toán để "playing with FLow Matching" nào!

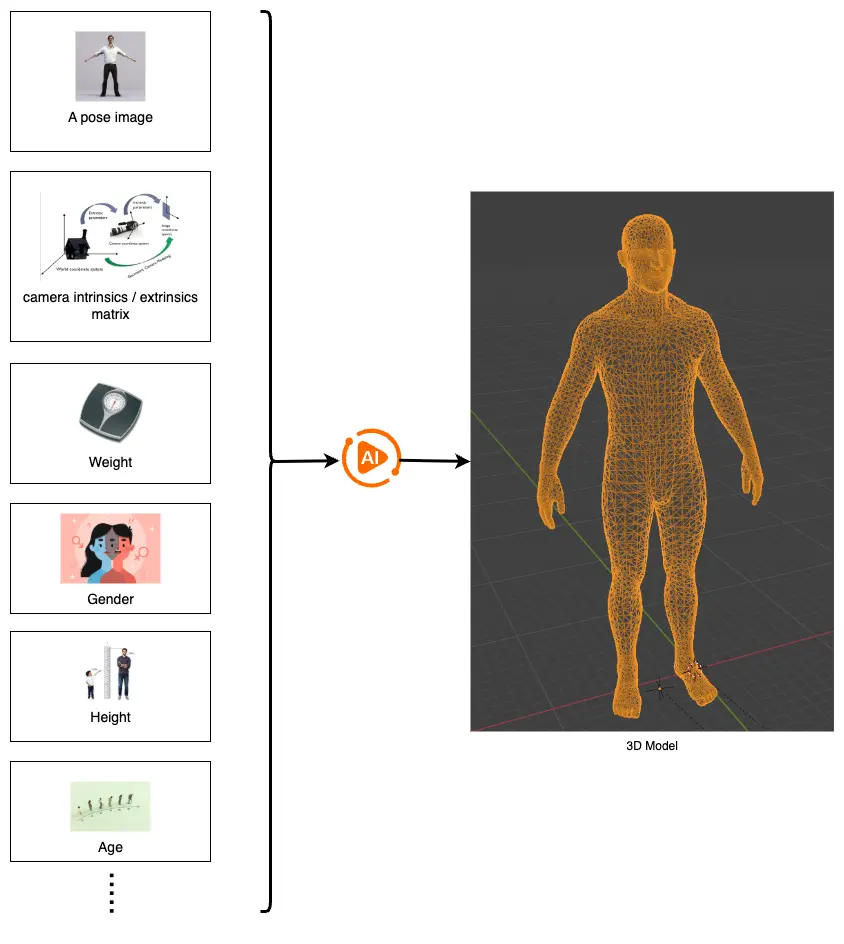
Vấn đề được lựa chọn thử nghiệm ở đây là: tạo mô hình 3D cơ thể người, chính xác về cả hình dạng và kích thước, với đầu vào là ảnh, chỉ số camera, cân nặng, chiều cao, giới tính, tuổi. ¹ Lựa chọn bài toán này là do cơ duyên biết đến nó thôi! Đầu bài có chữ "tạo", có vẻ phù hợp với tư duy GenAI nên thử suy nghĩ xem sao.

Đầu vào là các đại lượng quen thuộc, ngoại trừ chỉ số camera. Tại sao cần nó? Theo trực giác, nếu cần chính xác về mặt kích thước, hẳn là cần thông số camera để đo đạc! Tuy nhiên, như có thể thấy dưới đây, hoàn toàn có thể đánh giá và đo đạc trực giác này mà không cần võ đoán như này! Lý do tương tự với các đầu vào khác. Nghi ngờ về đầu vào ở đây không phải là một sự thừa thãi điên rồ, đây là sự khác biệt căn bản giữa thực tế vào trong sách. Vấn đề trong sách là đầy đủ và có giải được - do đã được người ra đề kiểm chứng. Vấn đề thực tế là của trời, của đất, không ai đảm bảo đầu vào bao nhiêu là đủ, cũng không ai đảm bảo là nó có thể giải được hay không. Độ vênh giữa thực tế và trong sách là rõ ràng, do vậy ta thường thấy sinh viên mới ra trường hay lóng ngóng - đặc biệt với các trường đào tạo quá lý thuyết. Lý thuyết không sai, nó chỉ là chưa được khai thác đủ trong bối cảnh của nó. Như ở đây, ta không chỉ phải tìm cách giải, ta còn phải tìm cách đánh giá đề bài, tự ra đề và tự giải.

Đầu ra là mô hình 3D cơ thể người - tập hữu hạn ($N$) điểm trong không gian 3 chiều. Tất nhiên $N$ điểm này không yêu cầu phải có thứ tự, cũng không yêu cầu $N$ là một số cố định. Vậy ta nên chọn $N$ cố định hay tuỳ ý, và liệu có cần thứ tự không? Lưu ý rằng đầu ra của bất kỳ một neuron network nào cũng luôn là cố định, vì vậy, lựa chọn $N$ cố định là biện pháp duy nhất? Không hẳn, điều này chỉ đúng nếu bắt buộc đầu ra của network là toạ độ các điểm trong model 3D! Bỏ điều kiện $N$ cố định đòi hỏi thêm một giải pháp đệm giữa đầu ra của network và kết quả cuối cùng. Có nhiều giải pháp để làm bước đệm này... chúng ta sẽ không đi quá sâu vào vấn đề này, đưa ra ở đây chỉ để thấy rằng, không có gì là ngẫu nhiên cả!

Tiếp tục với vấn đề thứ tự của các điểm trong mô hình 3D. Với con người thì thứ tự không quan trọng, vì chúng ta quan sát mô hình bằng góc nhìn toàn cục. Nhưng network thì không như vậy, nó phải sinh ra mô hình với từng điểm trong không gian 3D. Nếu dữ liệu huấn luyện có sự hỗn loạn về mặt thứ tự các điểm, sẽ gây hỗn loạn cho network để học ngữ nghĩa của từng đầu ra, vì trên cùng một node mạng đầu ra, ngữ nghĩa phải biến đổi theo từng bối cảnh? Đây tiếp tục là một trực giác cần được kiểm chứng. Ở đây, để đơn giản ta chọn các điểm đầu ra là có thứ tự (dẫn đến dữ liệu huấn luyện sẽ được yêu cầu phải có thứ tự)

Để thuận tiện, ký hiệu các đại lượng bằng các ký hiệu toán học như sau:

Đầu vào:

• Ảnh chụp 2D dáng chữ A (image): $I \in \R^{W \times H \times 3}$
• Thông số camera (camera matrix): $c \in \R^{3 \times 4}$
• Cân nặng (weight): $w \in \R$
• Chiều cao (height): $h \in \R$
• Giới tính (gender): $g \in \{0,1\}$
• Tuối (age): $a \in \R^+$

Đầu ra:

• Mô hình 3D gồm N điểm trong không gian 3 chiều: $y \in \R^{N \times 3}$

Từ đó, bài toán trở thành tìm hàm $f$ thoả mãn:

$$y = f(I,c,w,h,g,a)$$

Cách đơn giản nhất là xấp xỉ hàm $f$ bằng MLP network (Multilayer Perceptron). Sử dụng phương pháp này, ta chỉ cần thay đổi số lượng node mạng đầu vào và đầu ra cho khớp với yêu cầu hàm số $f$, sau đó huấn luyện với dữ liệu để học tham số của $f$. Vấn đề của MLP là nó quá linh hoạt, tức là không gian các hàm nó có thể xấp xỉ rất lớn, khiến việc huấn luyện trở nên khó khăn (Bias–variance tradeoff). Thực tế đã chứng minh rằng các mô hình khác, nhờ sự kém linh hoạt hơn (?!), mà dễ huấn luyện hơn và đạt được kết quả cao hơn. Và dưới một góc nhìn nào đó, Generative AI cũng là một cách để giảm độ linh hoạt mô hình trong quá trình huấn luyện!

Để xử lý bài toán của chúng ta dưới góc nhìn Generative AI, trước tiên chia bài toán thành hai bước:

• Bước 1: học cách generate ra mô hình 3D cơ thể người hợp lệ
• Bước 2: generate mô hình 3D hợp lệ với các điều kiện đầu vào (ảnh, tuồi, giới tính...).

Sau 2 bước, ta có mô hình 3D hợp lệ với điều kiện cho trước. Nhìn qua rất giống chiến lược kinh điển để giải quyết vấn đề: chia để trị. Việc gì khó thì cứ xé nhỏ ra làm từng bước, ắt thành công. Nhưng điều khác biệt ở đây là cách chia, chứ còn chia nhỏ thì đúng đường lối rồi!

Tại sao phải quan tâm đến sự hợp lệ của mô hình 3D trước?

Quan sát tập hợp các mô hình 3D cơ thể người, có thể thấy rằng tập hợp chứa các mô hình 3D hợp lệ có phân bố không đồng đều. Nhận định này khá hiển nhiên, vì mô hình 3D cơ thể người không phải là tuỳ ý, nó tuân theo một quy luật ẩn nào đó, trong toàn bộ quần thể loài người.

Ví dụ hình dưới là ví dụ một mô hình 3D ($y_{error}$) bất hợp lý vì cá điểm dữ liệu ở phần đầu đột ngột tách ra rất xa. Cá thể có xương sọ đột biến như vậy không hề tồn tại (hoặc ít nhất là không phổ biến). Và ta có thể dễ dàng tạo ra vô số mô hình 3D bất hợp lý như vậy bằng phương pháp trên. Từ đó có thể thấy rằng mức độ "tuỳ ý" của một mô hình 3D hợp lệ không hề cao mà chỉ tập trung ở một vùng hợp lệ rất nhỏ. Mục đích của bước 1 là khoanh vùng sự hợp lý này, nhờ đó mà công đoạn ở bước 2 trở nên ổn định hơn khi huấn luyện.

Với con người thì có thể dễ dàng nhận ra sự bất hợp lý này, nhưng lại không lượng hoá được. Điều gì xảy ra nếu phần mô hình lỗi chỉ hơi nhô lên "một chút" thay vì rõ ràng như hình, liệu mô hình 3D lúc này có còn hợp lý không?. Để dạy máy móc nhận ra và lượng hoá sự bất hợp lý này, người ta định nghĩa khái niệm xác suất.

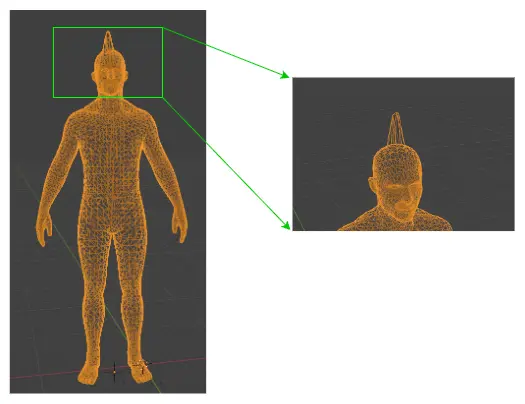
Xác suất một công cụ để đo lường sự bất hợp lý, hay sự không chắc chắn, không vì tại sao, chỉ vì nó được định nghĩa để làm điều đó. Trong ngôn ngữ xác suất, sự bất hợp lý trên được phát biểu là: xác suất sảy ra sự kiện tồn tại một người có mô hình 3D cơ thể như hình là thấp.

$$P(y_{error}) \backsimeq 0$$

Mục tiêu của chúng ta là sinh ra các mô hình 3D hợp lệ, trong ngôn ngữ xác suất thì hành động tương đương là lấy mẫu (sample) trong không gian mẫu của các mô hình 3D cơ thể người. Để làm điều đó, trực tiếp nhất là ta đi tìm công thức phân phối xác suất của nó, từ đó sẽ biết ở "vùng" nào thì mẫu ta lấy có xác suất cao (hình dưới)

Tập hợp các mô hình 3D cơ thể người nằm trong không gian $\R^{N \times 3}$ tức là có $3N$ chiều. Với N có thể lên tới hàng nghìn tuỳ vào nhu cầu về độ chi tiết đầu ra. (Đây được coi là một con số lớn đối với năng lực tính toán của các hệ thống tính toán hiện nay) Có một cách đơn giản để tìm công thức phân phối của một tập dữ liệu là: "chọn" dạng mô hình xác suất mà ta đã biết hoặc quen thuộc, đơn giản (ví dụ: Multivariate Gaussian) và thực hiện tối đa hoá khả năng (Maximum Likelihood Estimation) để tìm tham số phù hợp.

Rõ ràng vấn đề của phương pháp này là: phân phối thực chưa chắc đã là dạng đã chọn (Multivariate Gaussian), cố ép công thức của Multivariate Gaussian vào thì ta chỉ thu được một bộ chỉ số "gần đúng" kém chất lượng. Nếu không chọn Multivariate Gaussian thì ta cũng không có thông tin nào "dạng" mô hình xác suất mà dữ liệu thực đang tồn tại để lựa chọn.

Cách tiếp cận của Flow Matching (FM) với vấn đề này không quá chặt như trên. FM không ép buộc phân phối cần tìm phải có dạng cố định, thay vào đó nó sẽ tìm cách biến đổi "dần dần" một phân phối đơn giản thành phân phối cần tìm. Mục đích vừa là để phân phối đích có thể tuỳ ý, vừa là để chuyển việc lấy mẫu về thực hiện trên phân phối đơn giản hơn (dễ thực hiện hơn).

FM bắt đầu từ một phân phối khới tạo (mà ta đã biết cách lấy mẫu), sử dụng tính chất bảo toàn của hàm xác suất để biến đổi dữ liệu mẫu trong không gian xác suất khởi tạo sang không gian xác suất đích. Theo định nghĩa ban đầu của xác suất, bất cứ một hàm xác suất hợp lệ nào cũng cần thoả mãn:

$$\int^{+\infin}_{-\infin} f(x) = 1$$

Điều kiện này đóng vai trò như một ràng buộc mềm (soft constraints) để tối ưu hoá việc huấn luyện mô hình. Ràng buộc này được giữ trong toàn bộ quá trình biến đổi, biểu hiện như một sự bảo toàn dòng chảy của một chất lỏng, dẫn đến tên gọi của phương pháp này! Nguồn gốc của ý tưởng này có rất nhiều yếu tố lịch sử, từ các thuật toán suy giảm số chiều -> nén dữ liệu -> biến đổi dữ liệu, tóm lại là ý tưởng của rất nhiều người trong nhiều thập kỷ. Tức là rất khó để nói chính xác tại sao người ta lại nghĩ ra nó!

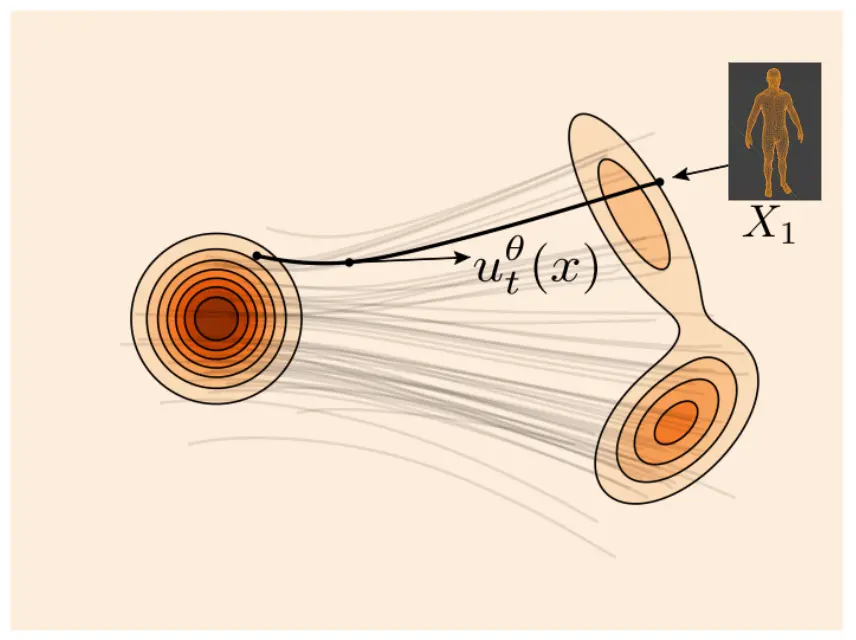
Như minh hoạ trên hình, việc lấy mẫu trên không gian khởi tạo đơn giản, nhanh chóng (do tính đối xứng và đã biết công thức phân phối). Sau khi huấn luyện mô mình với dữ liệu, ta có quy trình sinh mô hình 3D hợp lệ ($P_{data}$). Hay nói chính xác hơn là mô hình sinh mô hình 3D hợp lệ ngẫu nhiên. Bước tiếp theo là biến đổi mô hình này từ sinh hợp lệ ngẫu nhiên thành mô hình sinh hợp lệ có điều kiện. Tức là tìm hàm xác suất có điều kiện $P_{data}(\cdotp | I,c,w,h,g,a)$ Việc này được giải quyết đơn giản bằng việc sử dụng classifier-free guidance, hiểu đơn giản là sử dụng thêm nhãn của dữ liệu trong quá trình huấn luyện.

Đến đây, ta có thể giải quyết vấn đề đặt ra ở đầu bài, liệu các đầu vào đã là đủ hay chưa? liệu có thể sinh ảnh với ít đầu vào hơn không? Theo định nghĩa xác suất về các biến ngẫu nhiêu độc lập, nếu dữ liệu hoàn toàn phân phối độc lập với điều kiện, nếu và chỉ nếu:

$$P_{data}(\cdotp | \varnothing) = P_{data}(\cdotp | I,c,w,h,g,a)$$

Tức là điều kiện nào làm thay đổi phân phối xác suất ban đầu nhiều nhất, thì mức độ quan trọng và cần thiết càng cao! Điều này đúng với toàn bộ điều kiện, từng điều kiện hoặc từng nhóm điều kiện đầu vào. Ví dụ sau khi huấn luyện ta nhận được kết quả:

$$P_{data}(\cdotp | I,c,w,h,g) = P_{data}(\cdotp | I,c,w,h,g,a)$$

Có thể kết luận là mô hình 3D cơ thể người không phụ thuộc vào tuổi tác! Đặc biệt là nếu sử dụng Kullback-Leibler (KL) divergence hoặc Cross-Entropy để định lượng sự khác biệt giữa hai phân phối, ta có thể đánh giá mức độ phụ thuộc của từng điều kiện đầu vào. Từ đó đưa ra lựa chọn với những mức độ chính xác khác cho người dùng thay vì ép buộc cần mọi điều kiện đầu vào.

Tóm lại ta có loss function như sau:

$$\pounds^{CDG}_{CFM}(\theta) = \Bbb{E}_{\square}|| u^{\theta}_{t}(y|I,w,h,g,a) - u^{target}_{t}(y|I,c,w,h,g,a)||^2 \\[0.2in] \square = \begin{cases} (y,I,w,h,g,a) \text{\textasciitilde} p_{data}(y,I,c,w,h,g,a) \\ t \text{\textasciitilde} \text{Unif}[0,1) \\ x \text{\textasciitilde} p_t(\cdotp | z) \\ \text{replace} \space I,c,w,h,g,a = \varnothing \space \text{with prob.} \space \eta \end{cases}$$

Với dữ liệu mô hình 3D đầu vào, tiền xử lý dữ liệu đầu vào có thể giảm tải cho việc học của mạng. Mô hình 3D cơ thể người là bất biến với các phép biến đổi dịch chuyển, vì vậy có thể dùng chiến lược chuẩn hoá hệ trục toạ độ, sao cho vẫn giữ được thông tin về độ lớn của mô hình. Một chiến lược khác là thiết kế các layer trong mạng neuron sao cho đầu ra là bất biến với các phép dịch chuyển trong không gian, như ý tưởng của CNN.

Trên đây chỉ là một ý tưởng chỉ ra cách áp dụng Flow Matching, mục tiêu là giúp ace xây dựng trực giác về phương pháp này khi trong thực tế, hy vọng khi ace nhìn thấy vấn đề khác mà có tính "tương tự", có thể nghĩ đến phương hướng giải quyết này!

Khoá học tham khảo: Link

Lưu ý:

Footnotes

1. Đầu vào có thể mở rộng thêm quốc tịch, màu da, màu tóc..... nhưng để ngắn gọn chỉ chọn các biến trên. ↩